hyperbolic genre embeddings for music classification
is the title of my master's thesis in music technology, which i completed under the advisement of Dr. Juan Pablo Bello and Dr. Brian McFee, at different times. i had a ton of fun working on this project, so i wanted to commemorate it at least somewhat with a more informal run-through of my goals and approach.
i investigated whether hyperbolic embeddings of music genres obtained from co-occurrence data can be used for music classification tasks. the answer i arrived at was... it seems probable, with further research certainly remaining interesting!
motivation, background, etc.
music genre classification and discussion is one of my personal obsessions. i spend a lot of time thinking about why we talk about music with the language that we do; why it matters to us as listeners in the first place; and how we decide how music is related to other music. these are, perhaps unsurprisingly, pretty challenging questions to answer. and spending a lot of time on rateyourmusic is not actually as productive as one might hope. sigh.
in any case, there's been a veritable wealth of investigation into several of these questions over the past few decades in music information retrieval (MIR) research. the bottom line, roughly, is that music genre classification is really hard, in the best case. there are a bunch of reasons for this, but perhaps the most important is that genres labels are both subjective and editorial [1] .
there's no expectation for humans to agree on the "true" genre label for a piece of music, and we often don't (...such is the plight of the aforementioned rateyourmusic). moreover, it's not just nice audio features (things like pitch, timbre, and tempo) by which we designate the "correct" genre label for a piece of music -- it's all sorts of extramusical characteristics as well. things like lyrics, cover art, geographical information.
so the attention then necessarily sort of turns to how we best approximate the popular opinion of genre labeling -- not only the descriptors that are often used in the real world, but also the relationships between them. it would be better, after all, to misclassify a genre as something kinda similar, than dubiously related at all. that is, having a notion of incorrectness in genre classification is important.
hyperbolic embeddings
to attempt to work towards this goal, i wanted to investigate graph embeddings of a co-occurrence matrix of music genres—representing, in essence, when genre $i$ appears alongside genre $j$ in common usage. if "rock" as a label commonly shows up alongside "heavy metal," we want to capture that. in particular, i used co-occurrence data from the Spotify API, based on curated genre playlists from the husk of the every noise at once project, started by glenn mcdonald probably before i was sentient.
this project contained an algorithmically-curated playlist full of 100 songs which are representative of the 6,291 genre tags in the Spotify dataset, based on popularity, listener patterns, and so on. from these tracks, i scraped the genre information from each associated artist (since Spotify assigns genre labels at the artist level). i then created a directed adjacency matrix for this data, by taking a connection from $i$ to $j$ to mean that on the playlist for genre $i$, genre $j$ also appears at least once. each connection was also weighted by the number of co-occurrences; so if "pop" appears 43 times in the "rock" playlist, the edge from "rock" to "pop" would have a weight of 43. relatively self-explanatory, i hope.
the co-occurrence matrix for music genres has entries $A_{\set{i,j}}$, which represent directed connections from genre $i$ to genre $j$. in most cases, we also disregard auto-adjacency, meaning that $A_{\set{i,i}} = 0$. note also that this matrix isn't necessarily symmetric; $i \to j$ does not imply $j \to i$.
Astefanoaei & Collignon [2] , whose work i expanded on for this project, showed that the co-occurrence matrix is a capable representation of hierarchical relationships in genres. this is essentially because we take that genre $i \to j \neq j \to i$, which is the relationship that all genre $i$ is $j$, but not all $j$ is $i$. consider "rock" and "pop rock"; all "pop rock" is probably "rock," but the other way around is not necessarily true.
great! so what do we do with this? well, we can stick it into a poincaré embedding model, such as the seminal work by Nickel & Kiela [3] , which takes exactly this graph representation and tries to embed it in hyperbolic space. this hyperbolic space has the property of consistent negative curvature; as we get further out from the center of the space, there's basically "more space" for points (embeddings) to exist. the bottom line here is that hyperbolic space is the analog equivalent of a tree structure; in other words, exactly what we're trying to represent. great!
hybrid cross-entropy loss
the main thing i wanted to test with this work was whether we could usefully leverage these embeddings as some sort of a weighting scheme within classification tasks—specifically, in a way that would allow us to generically apply a large, pre-computed embedding space onto arbitrary classification models. to test this, i roughly borrowed a training pipeline from the NLP world, specifically from the work of Chen et al. [4] on emotion classification in text representations.
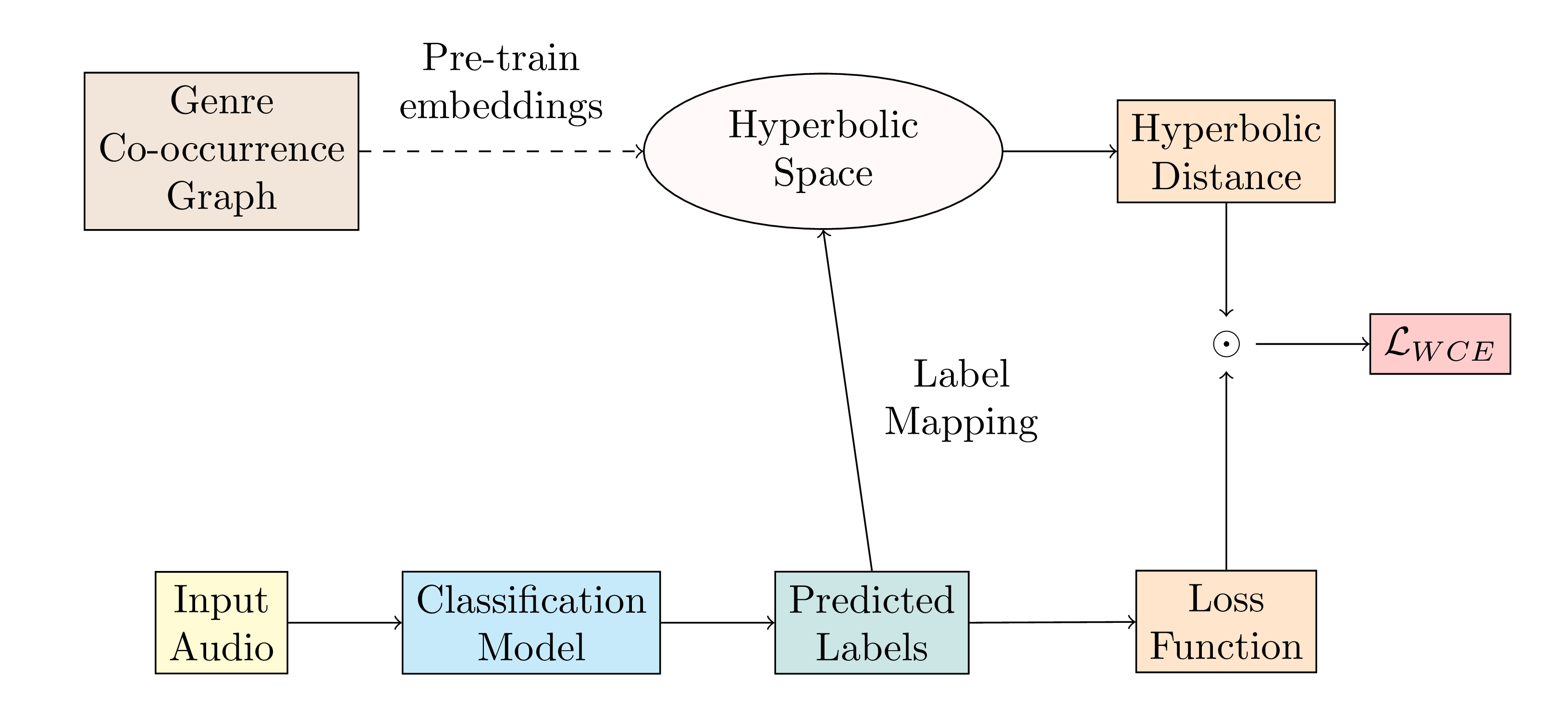
the goal of this pipeline was basically just to shove the structure of the hyperbolic space into a normal, boring training paradigm—and hopefully investigate at sort of the barest level whether the structure of the space might provide any interesting benefits to classification tasks. to do this, i took the approach from Chen et al.'s work of adding a weighting term $w_i$ to the classical cross-entropy loss function:
\begin{equation} \mathcal{L}_{CE} = \frac{1}{N} \sum_{i=1}^{N} - \log \frac{\exp(c_{i}^{y_i})}{\sum_{j=1}^{k} \exp(c_i^j)} \end{equation}
\begin{equation} \mathcal{L}_{WCE} = \frac{1}{N} \sum_{i=1}^{N} -\textcolor{red}{w_i} \log \frac{\exp(c_{i}^{y_i})}{\sum_{j=1}^{k} \exp(c_i^j)} \end{equation}
this term just comes from the hyperbolic distance between genre embeddings in poincaré space:
\begin{equation} w_i = d(y_i, \hat{y}_i) = \cosh^{-1}\left( 1 + 2\frac{\lVert y_i - \hat{y}_i \rVert ^2 }{(1 - \lVert y_i \rVert ^2)(1 - \lVert \hat{y}_i \rVert ^2)} \right) \end{equation}
the embeddings in question
even outside of the question of genre classification, replicating the results from Astefanoaei and Collignon's paper was pretty cool. there are some interesting insights here already:
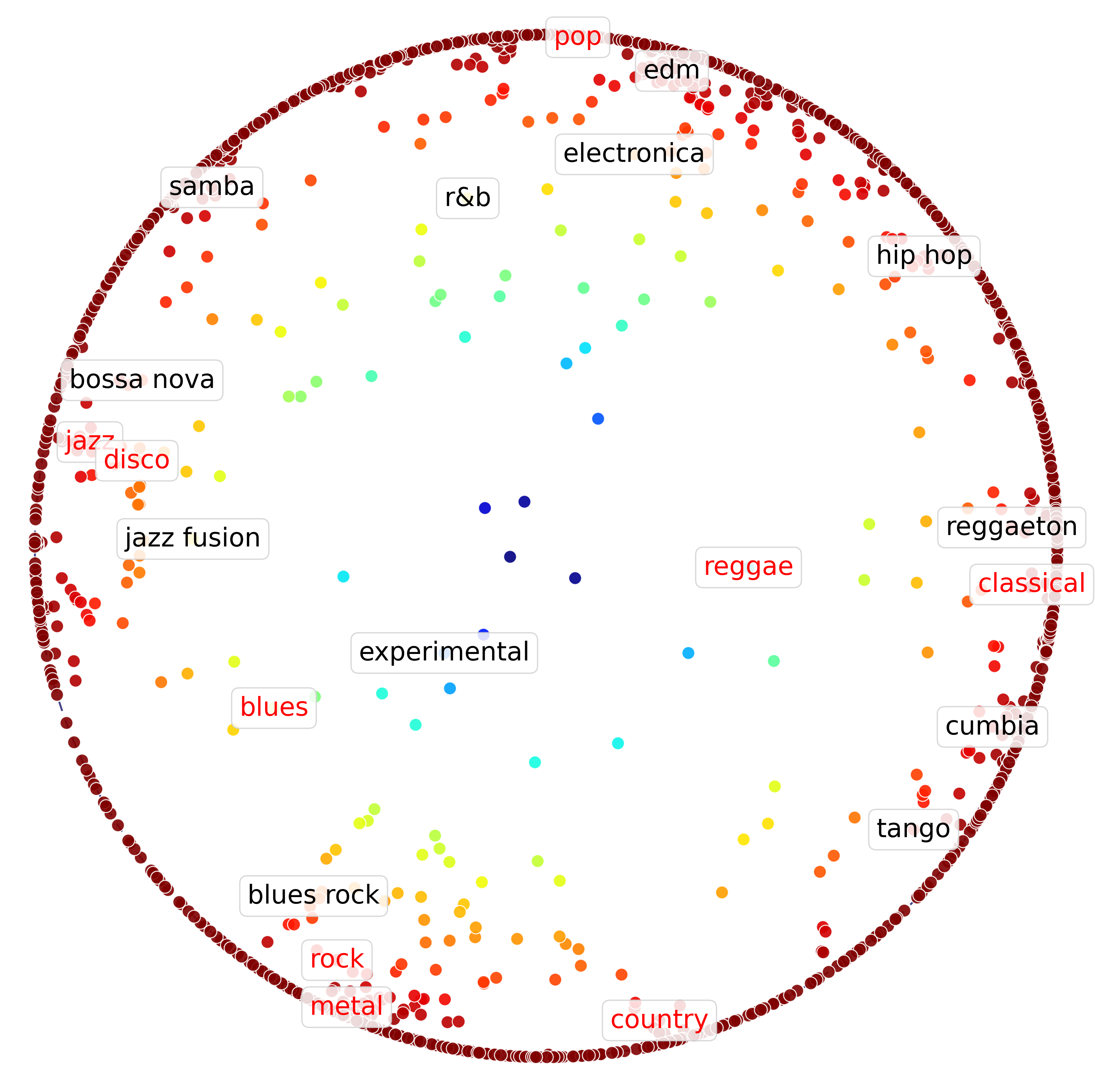
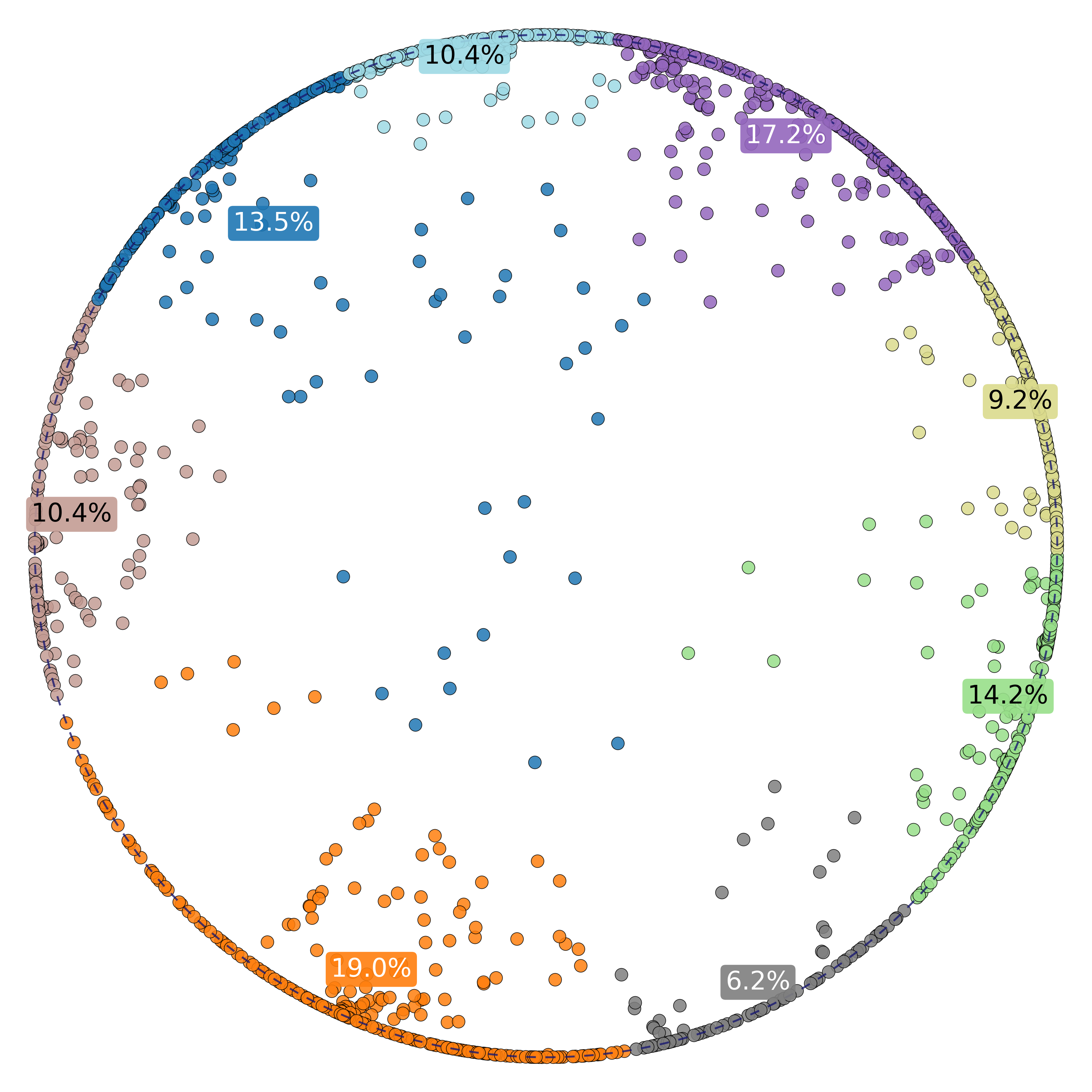
for one, we see some key semantic clusterings that we hoped would show up in these embeddings; for example, "rock" and "metal" end up next to each other, as do "jazz" and "disco", and the high-level genres that are highlighted in fig 3 are spread relatively evenly around the poincaré disk. cool! we also see that these high-level genres roughly adhere to the hierarchical clustering analysis in fig 4.
these embeddings also outperform Word2Vec, a similar "sentence embedding" model that embeds the exact same data (co-occurrence of words in sentences, with directionality encoded by position in the sentence). A t-SNE plot of those embeddings looked like this:
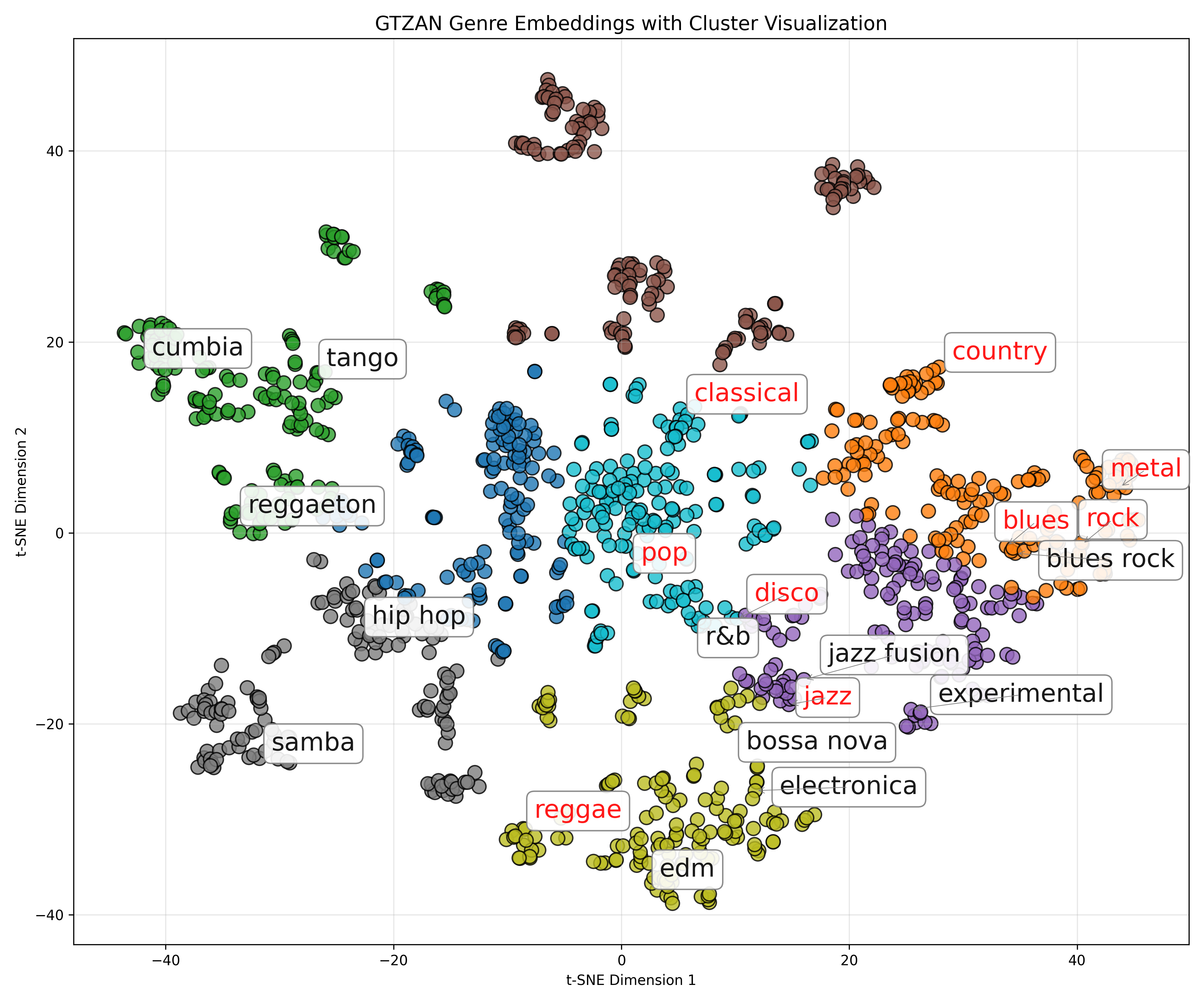
i found, as expected (and hoped!) that every dimensionality of the poincaré embeddings outperformed the Word2Vec embeddings on mean rank and mean average precision metrics.
probing the structure
so one of the cooler aspects of this whole project was the ability to navigate the embedding space directly. what this allowed me to do was to create a constrained $k$-nearest neighbor retrieval search on the embedding space to try and isolate genre labels which had specifically parental relationships to the query label.
to do this, i simply constrained the KNN search to embeddings with a lower norm (i.e. closer to the center of the poincaré ball/disk) and small angular distance between embeddings. this is because the lower-norm direction encodes the generality of a certain label, which is correlated with parental relationships. the example i used in my presentation was the label "queens hip hop," which is a relatively semantically complex label; it's got not only stylistic meaning, but also geographical information and an explicit reference to a parent genre.
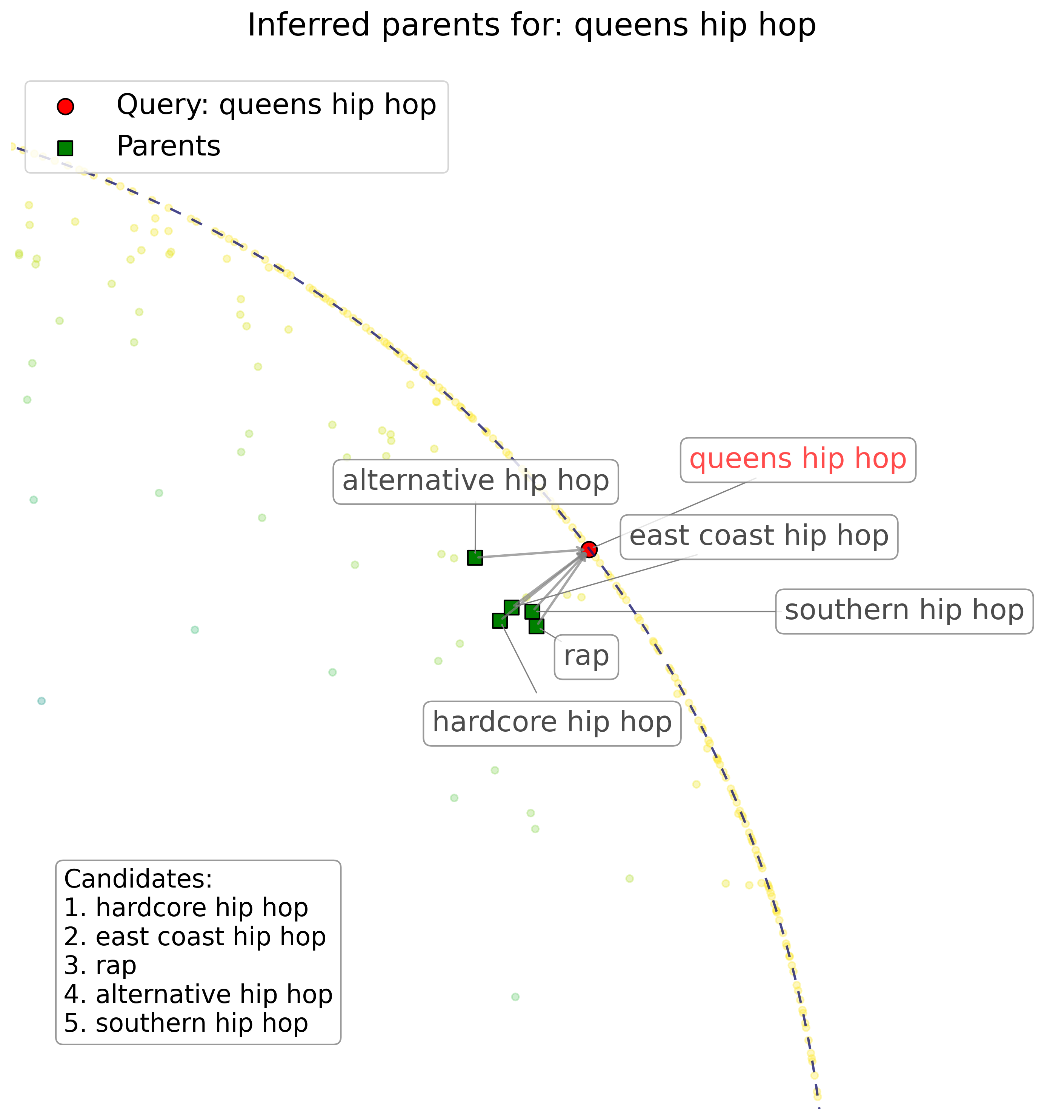
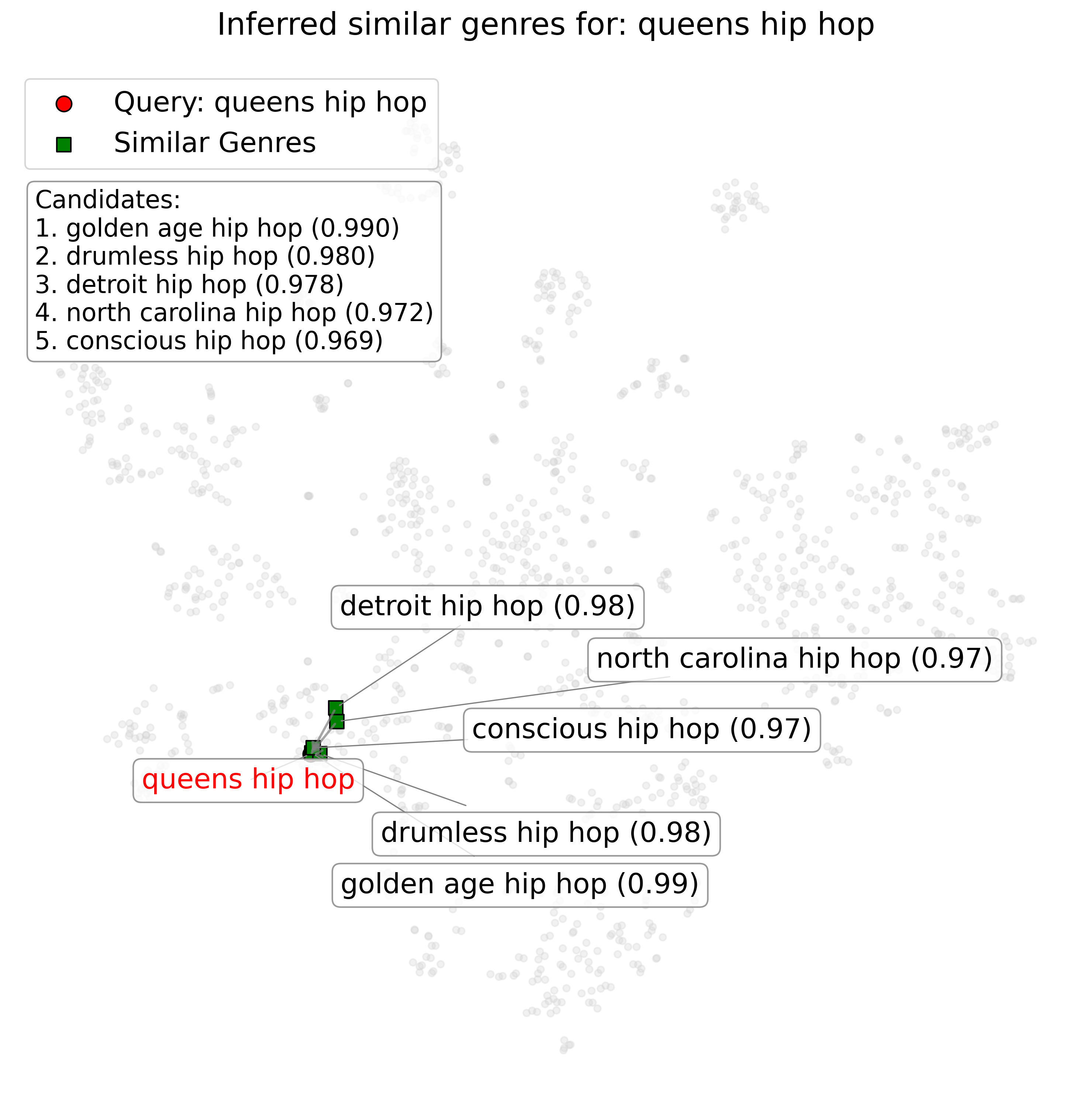
an interesting note about the difference between the hyperbolic embeddings and the Word2Vec embeddings is that the Word2Vec embeddings with a pure KNN search find similar genres both in style (e.g. drumless hip hop, conscious hip hop) and in other semantic relationships, such as other genres with geographic information (e.g. detroit hip hop, north carolina hip hop). whereas the hyperbolic embeddings, just as we hoped, not only successfully retrieve more general parentally-related genres (e.g. rap) but also genres with semantically parental relationships, such as east coast hip hop. kinda neat!
classification performance
sadly, i didn't have quite as much time during the course of my thesis work to dig deeply into the classification implementation as i had hoped. as such, the performance improvements with my current implementation were pretty marginal. below are two of the confusion matrices, from a fine-tuned transfer learning model called YAMNet:
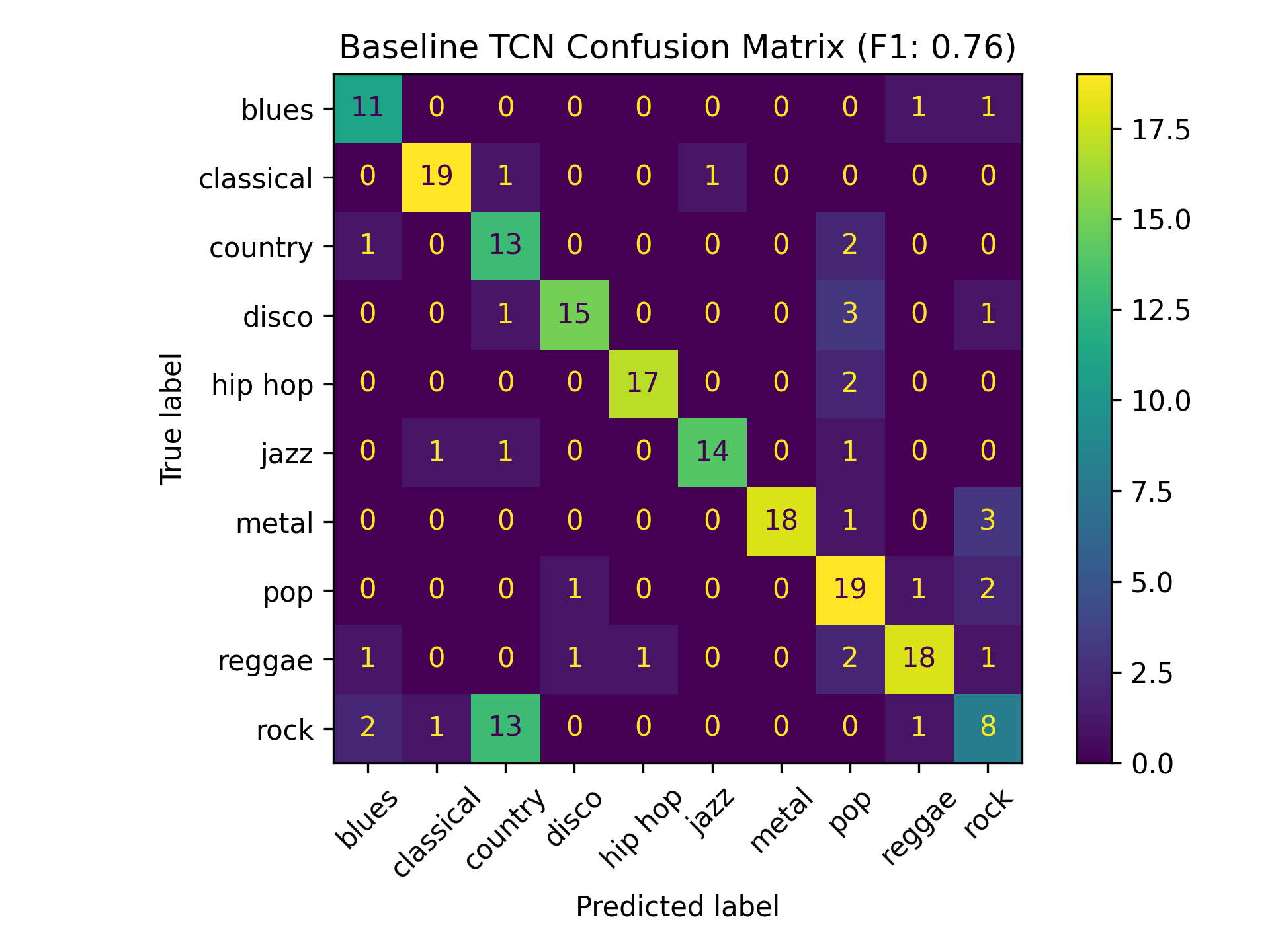
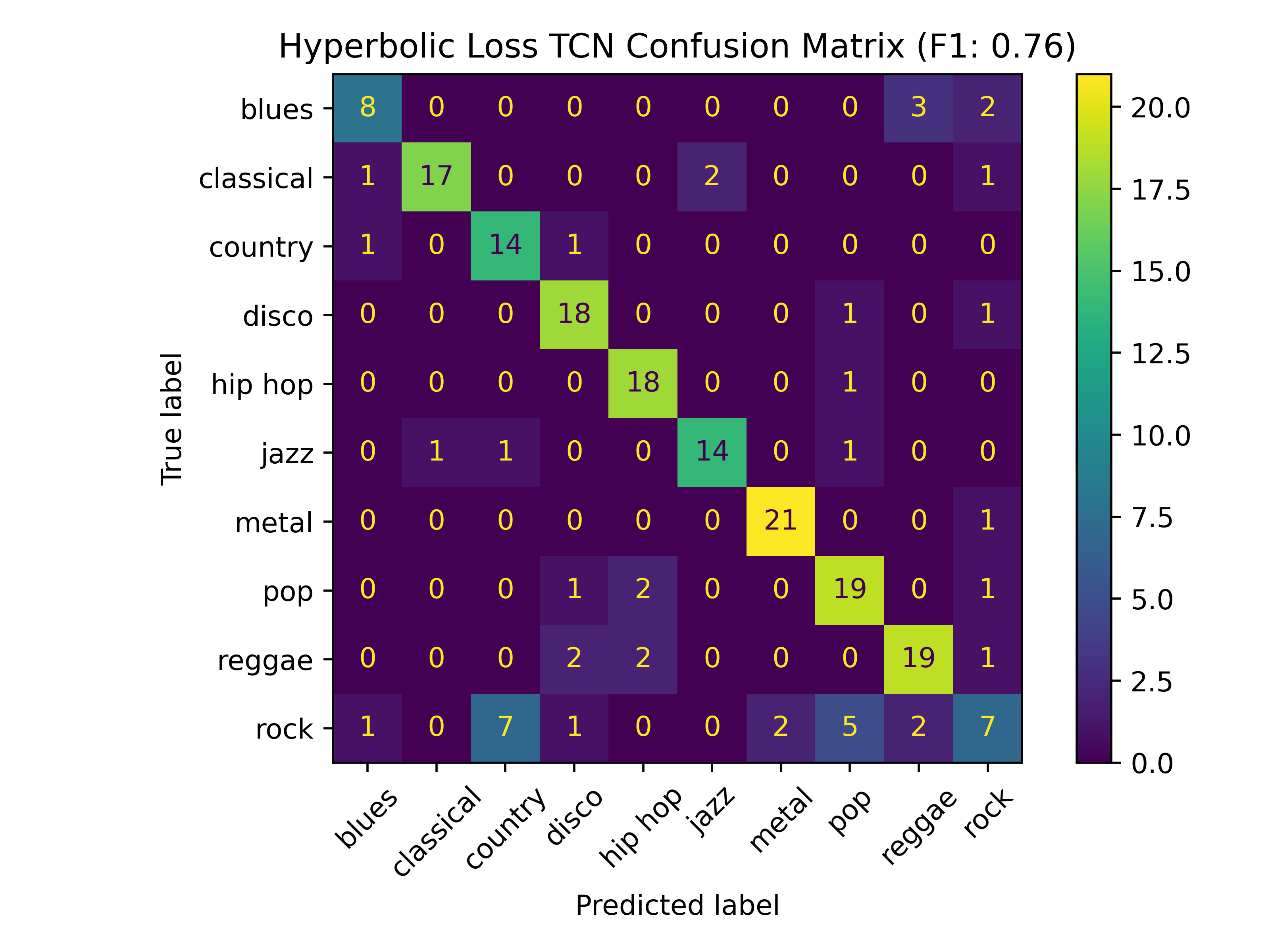
as you can see, the differences are not too overwhelming. and in fact, the F1-score between the two models was identical in this case, using 10-dimensional Poincaré embeddings. the one thing i did note between these two confusion matrices was that the commonly-confused label pair of "country" and "rock" were spread into several different labels when using the hybrid loss function. but the real insight, it seemed, came from investigating the per-class performance:
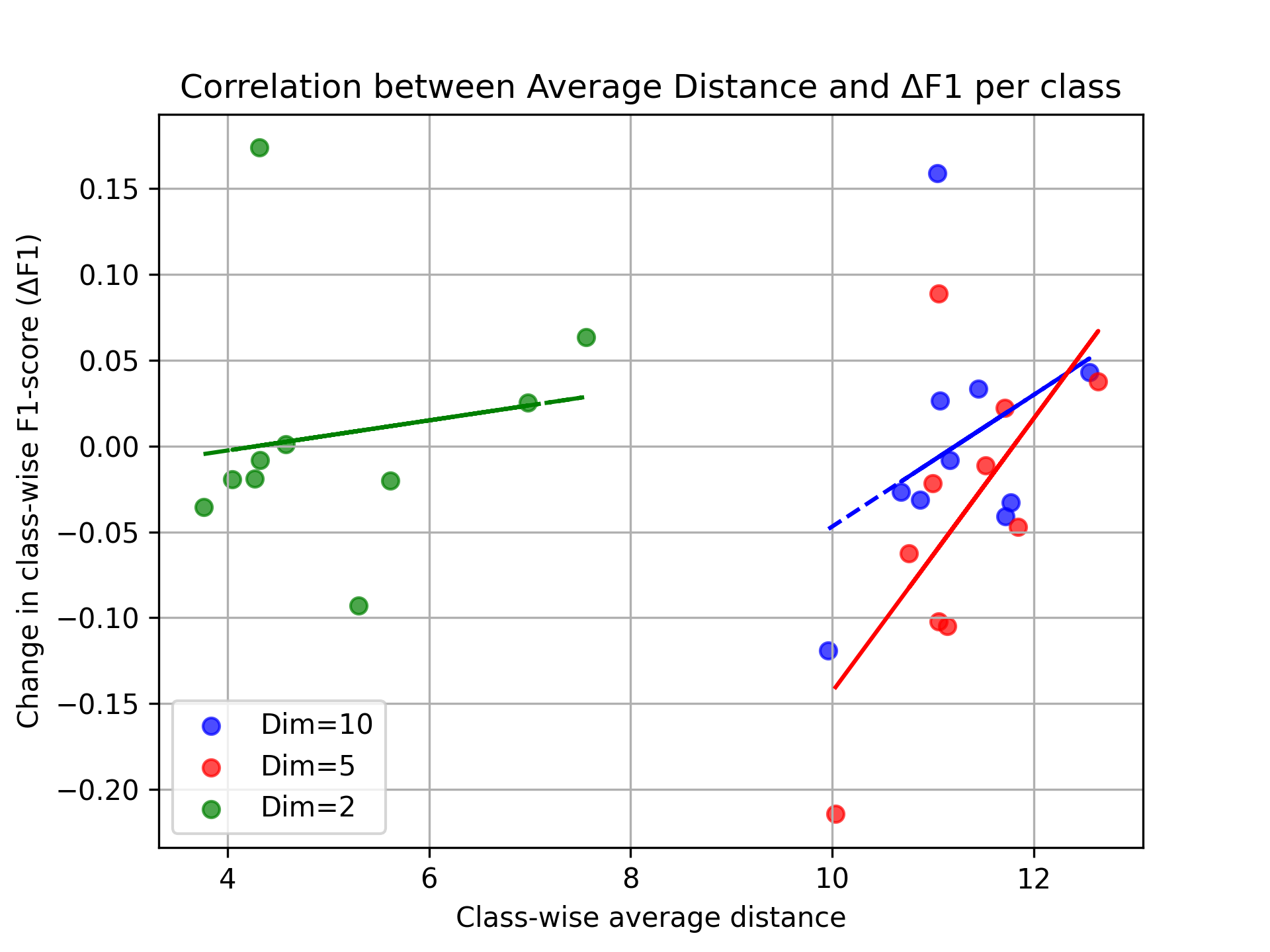
what this shows is a pretty consistent per-class improvement in F1-score. this suggests that labels which exist farther apart in the embedding space see heightened performance on classification tasks, while there is some confusion introduced by labels which have a low average distance and are central to the other embeddings. this further suggests that the structure learned from the embedding space is beneficial to classification accuracy when distinguishing genres that are semantically unique from other genres in the same dataset. this positive trend suggests that while the current implementation may not be optimal, the structure of the embeddings could be used in other ways to separate genre labels which are confused by classification models.